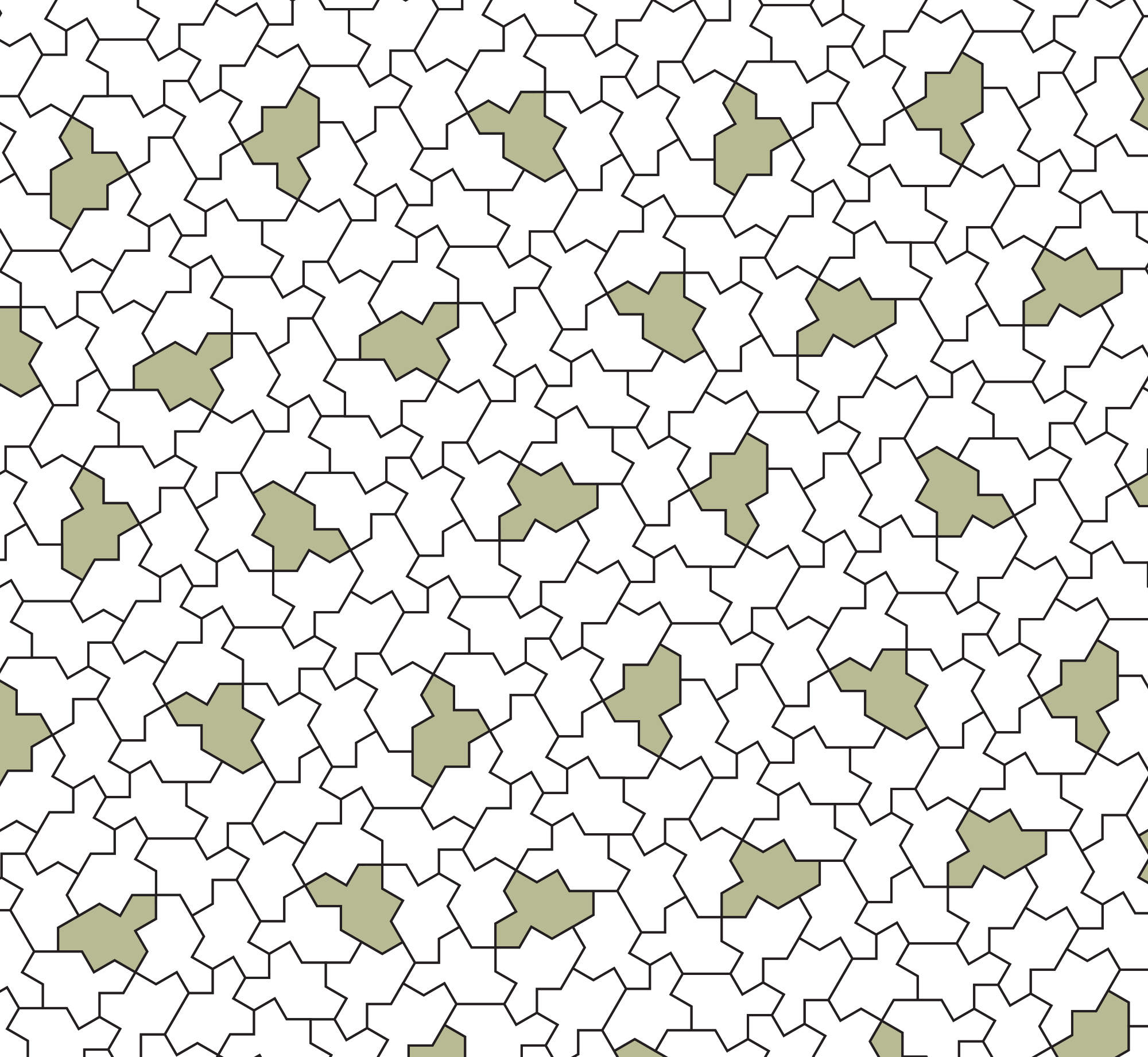
Two months ago I blogged about the resolution of the famous problem whether a single shape can tile the entire plane, but only aperiodically (link). There was just one drawback to the solution: It required not only translating and rotating the shape, but also reflecting it.
In a recent preprint (arXiv:2305.17743) this drawback was overcome now: A new shape (a modification of the previous one) that tiles the plane aperiodically using only translations and rotations, and even if you allow reflections it can not tile periodically.
Here is a webpage (by one of the authors) with some resources about this and from where I got the picture below: link. And here is another blog post with some information: link.