In a recent preprint (arXiv:2108.08506), Yosuke Kubota proved an intriguing new result on the relation of largeness properties of spin manifolds and index-theoretic obstructions to positive scalar curvature (psc):
Let \(M\) be a closed spin \(n\)-manifold. If \(M\) has infinite \(\mathcal{KO}\)-width, then its Rosenberg index \(\alpha(M) \in \mathrm{KO}_n(\mathrm{C}^\ast_{\max} \pi_1 M)\) does not vanish.
Let us briefly discuss the relevant terms. The Rosenberg index is a sophisticated version of the Fredholm index of the Dirac operator which takes the fundamental group into account. It is the most general currently known obstruction to the existence of positive scalar curvature metrics that is based on index theory of Dirac operators.
To understand \(\mathcal{KO}\)-width, a bit more elaboration is necessary. In recent years, Gromov proposed a number of new ideas involving quantitative distance estimates in the presence of lower scalar curvature bounds (see Metric Inequalities, Four Lectures). This includes the band width conjecture which can be formulated as follows.
Let \(V\) be a band that does not contain a hypersurface \(N \subset V^\circ\) such that
– \(N\) admits a metric of positive scalar curvature,
– \(N\) separates \(\partial_- V\) from \(\partial_+ V\).Then \(V\) satisfies the band width estimate, that is, if \(g\) is a Riemannian metric on \(V\) of scalar curvature \(\geq n(n-1)\), then
\[\mathrm{width}(V,g) := \operatorname{dist}_g(\partial_- V, \partial_+ V) \leq \frac{2 \pi}{n}.\]
Here a band is a connected compact \(n\)-manifold \(V\) together with a decomposition of the boundary \(\partial V = \partial_- V \sqcup \partial_+ V\) into two parts, where \(\partial_\pm V\) are unions of components.
While the main motivation of this conjecture is to understand scalar curvature from a concrete comparison geometry point of view, it can also be used in a qualitative way to obtain potentially new psc obstructions.
To this end, fix any class \(\mathcal{V}\) of bands. If \((M,g)\) is a Riemannian manifold, then one defines its \(\mathcal{V}\)-width, denoted by \(\operatorname{width}_{\mathcal{V}}(M,g) \in [0,\infty]\), as the supremum of all real numbers \(\operatorname{width}(V,\varphi^\ast g)\), where \(V \in \mathcal{V}\) and \(\varphi \colon V \to M\) is a local diffeomorphism. If the band width estimate holds for every band in \(\mathcal{V}\), and the scalar curvature of \((M,g)\) is bounded below by \(\kappa n(n-1)\) for some \(\kappa > 0\), then we must have \(\operatorname{width}_{\mathcal{V}}(M,g) \leq \frac{2 \pi}{\sqrt{\kappa} n}\). On the other hand, if \(M\) is compact, then whether or not \(\operatorname{width}_{\mathcal{V}}(M,g) = \infty\) does not depend on the Riemannian metric \(g\).
We thus deduce the following observation:
Let \(\mathcal{V}\) be a class of bands that satisfy the band width estimate. If a closed manifold \(M\) has infinite \(\mathcal{V}\)-width, then \(M\) does not admit a metric of positive scalar curvature.
Let us now discuss two important choices for \(\mathcal{V}\).
- The class \(\mathcal{T}\) of overtorical bands. We say \(V\) is overtorical if there exists a smooth map \(V \to \mathrm{T}^{n-1} \times [-1,1]\) taking \(\partial_\pm V\) to \(\mathrm{T}^{n-1} \times {\pm 1}\) of non-zero degree.
- The class \(\mathcal{KO}\) which consists of spin bands \(V\) such that the higher index \(\operatorname{Ind}_{\pi_1 V}(D_{\partial_\pm V}) \in \mathrm{KO}_n(\mathrm{C}^*_{\max} \pi_1 V)\) does not vanish. (This kind of index obstruction is built in such a way that it yields an index-obstruction on \(V\) which obstructs PSC on every separating hypersurface!)
Both of these classes satisfy the band width estimate (see Metric Inequalities, Band width Dirac, Long neck, Width Largeness).
Infinite overtorical width for a closed manifold is equivalent to being iso-enlargeable, a notion recently defined by Gromov which slightly generalizes Gromov and Lawson’s classic notion of enlargeability. Every overtorical band which is spin is contained in \(\mathcal{KO}\). In particular, all iso-enlargeable (and thus enlargeable) closed spin manifolds have infinite \(\mathcal{KO}\)-width.
Infinite \(\mathcal{KO}\)-width appeared initially quite intriguing because it was not a priori clear that it implies non-vanishing of the Rosenberg index although it is clearly based on index theory. However, motivated by a meta-conjecture of Thomas Schick on index-obstructions to psc (arXiv:1405.4220, Conjecture 1.5), I conjectured in Band width Dirac that this should indeed be the case. Kubota’s new theorem now confirms this!
Another interesting observation is that Kubota’s theorem yields a new proof of the fact that (length-)enlargeable manifolds have non-vanishing Rosenberg index, a theorem originally due to Hanke and Schick. At the moment we thus have arrived at the following implications:
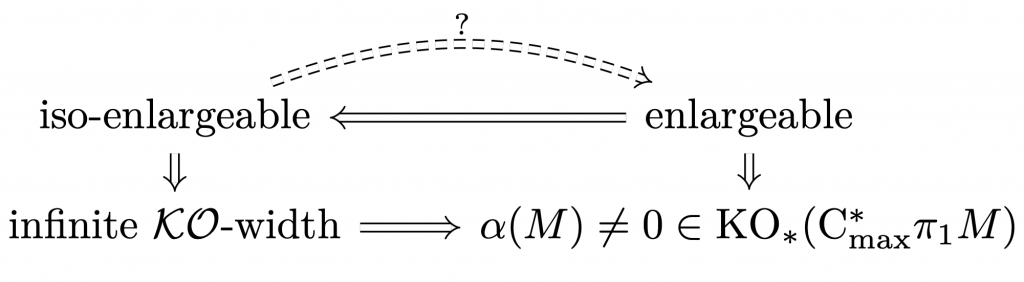
Here for the bottom row to make sense we need to assume \(M\) to be spin. The question of whether “iso-enlargeable” and “enlargeable” are the same condition remains an open problem.