An extremely classical theorem from planar geometry is the following one: If \(B_1\) and \(B_2\) are two strictly convex, compact planar domains with smooth boundaries touching at some point \(p \in \partial B_1 \cap \partial B_2\) with common inner normal, then \(B_1 \subset B_2\) provided that the curvatures \(k_i(\nu)\) of the boundaries satisfy \(k_1(\nu) \ge k_2(\nu)\) for all \(\nu\).
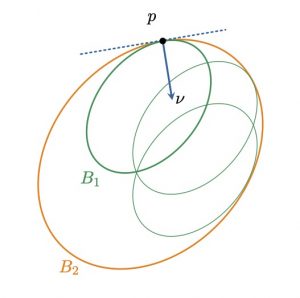
(source: Drach’s preprint)
Usually, such classical theorems get generalized to the setting of Riemannian manifolds. In the case of Blaschke’s inclusion theorem, it took quite a while: Only recently a version of it for Riemannian manifolds was posted on the arXiv by K. Drach (arXiv:2404.02739).