The countless shapes of snowflakes have long raised the curiosity of many scientists, among others the famous Kepler. They have by now been classified by empirical observation into 80 different shapes, but a mathematical explanation for this classification seems to be missing. A striking point about them is that, even though two snowflakes are almost never alike, they all share certain characteristics such as a six-fold symmetry.
Let’s look at a simple mathematical procedure to generate such a pattern, called Koch’s curve. In a polygon, whenever we encounter a line let’s replace it according to the following rule:
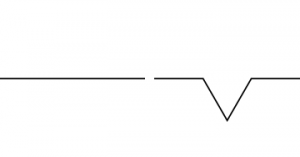
The result is again a polygon and we may iterate this step again and again. Here are two examples:

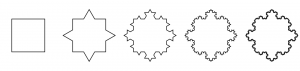
While this does look similar to an actual snowflake, it only accounts for a single shape. Of course, in nature the entire process takes place in reverse. It starts with a microscopic piece of ice and gradually over time, molecules attach to it. The rules for this attaching are probabilistic and depend on the outside temperature and pressure. Since every snowflake undergoes a unique trajectory of outer circumstances, this accounts for their individuality.
Roughly, the formation in nature can be described as follows. The hydrogen atom has its positive and negative poles arranged like the vertices of a tetrahedron. Under cold weather conditions, this leads to a tendency of hydrogen atoms to form hexagonal ice molecules. The result is a structure of ice similar to that of a honey comb. Now the electromagnetic forces favor some of its faces to grow faster than others, which leads again to hexagonal shapes on larger scales. This is how the six-fold symmetry can be explained.
For a detailed discussion from the point of view of chemistry, the following link is highly recommended reading: