Singmaster’s conjecture is an easy to state conjecture about Pascal’s triangle.
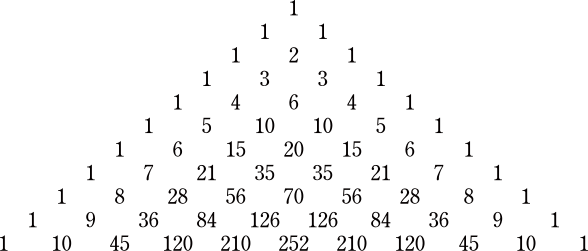
It is easy to see that every natural number in Pascal’s triangle occurs only a finite number of times. The conjecture of Singmaster now claims that there is actually a global upper bound on this number of occurrences!
The highest number of occurrences currently known is 8. In fact, there is only one such number known that appears exactly eight times, namely 3003. There are also no numbers known that appear exactly five or seven times. But there are infinitely many that appear exactly six times.
I am again baffled by combinatorial number theory: There are so many conjectures in this field that are extremely easy to state but are still unproven.
I learned about this conjecture by a blog post of Terence Tao on his own blog. There he reported on recent progress on this conjecture (arXiv:2106.03335).